Windows formを使ってグラフに沿って動く物体を描画する
Windows formを使って弾幕シューティングゲームを作ろう(シリーズ)。今回は「円の公式」を使って円形のグラフを描きます。敵キャラや弾幕に円運動が加わることで、直線的な動きよりも格段に面白さがアップしそうですね。
円の公式では平方根(ルート)が出てくるので、C#のMathクラスを利用します。自動的に動く物体を作るため、Windows
Formのフレーム関数を利用します。
目次 Table of Contents
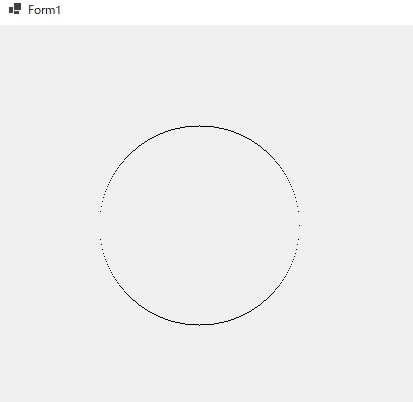
円の公式を使って円形のグラフを描く
数学の円の公式を使って円形のグラフを描画します。円の公式は
x2 + y2 = r2
ですね。これをy = の式に直すと
y = √(r2 – x2)
になりますね。ただしxの取りうる範囲は -(半径) ≤ x ≤ 半径
となることと、yの正負を考慮しないといけないのでちょっとめんどくさいですね。
public partial class Form1 : Form
{
Point start;
Bitmap p;
float radius;
public Form1()
{
InitializeComponent();
start = new Point(200, 200);
p = new Bitmap(1, 1);
radius = 100;
}
protected override void OnPaint(PaintEventArgs e)
{
//Graphicsオブジェクトを取得
Graphics graphics = e.Graphics;
p.SetPixel(0, 0, Color.Black);
//0 <= x <= radius
for (int i = 0; i <= (int)radius; i++)
{
//yが正の数
graphics.DrawImage(p, i + start.X, (int)(Math.Sqrt(Math.Pow(radius, 2) –
Math.Pow(i, 2))) + start.Y);
//yが負の数
graphics.DrawImage(p, i + start.X, (int)-(Math.Sqrt(Math.Pow(radius, 2) –
Math.Pow(i, 2))) + start.Y);
}
//-radius <= x <= 0
for (int i = (int)radius; i >= (int)-radius; i–)
{
//yが正の数
graphics.DrawImage(p, i + start.X, (int)(Math.Sqrt(Math.Pow(radius, 2) –
Math.Pow(i, 2))) + start.Y);
//yが負の数
graphics.DrawImage(p, i + start.X, (int)-(Math.Sqrt(Math.Pow(radius, 2) –
Math.Pow(i, 2))) + start.Y);
}
}
}
フレーム関数を使って時間とともに動く物体を作る
前章までで、ループを使って直線、放物線、円グラフを描画しました。今の状態ではグラフの全貌がすべて表示されてしまい、動きの表現になっていません。「直線的に下に落ちてくる敵キャラ」や「円を描きながらだんだん広がっていく弾」といったように、時間の経過とともにグラフの軌跡を辿って位置が変化するようなコードに変えてやる必要があります。
そこでWindows
formのUpdateメソッド(関数)を利用します。Updateメソッドは任意の時間が経過するごとに呼び出されるフレーム関数と呼ばれるもので、ゲームやアニメーションを作るのに必要なメソッドです。アクションゲームやシューティングゲームなどでは、ゲーム実行中に常に一定サイクルで関数を呼び出すような仕組みになっていて、そこで動くオブジェクトの瞬間的な位置を決めたり、パラパラ漫画の1コマを表示させたりします。
public partial class Form1 : Form
{
Point start;
Pen pen;
float r;
int x;
public Form1()
{
InitializeComponent();
start = new Point(40, 40);
pen = new Pen(Color.Black, 1);
r = 8; //物体の半径
x = 0;
//Timer
Timer timer = new Timer();
timer.Interval = 16;
timer.Tick += new EventHandler(Update);
timer.Start();
}
private void Update(object sender, EventArgs e)
{
Invalidate();
x++;
}
protected override void OnPaint(PaintEventArgs e)
{
//Graphicsオブジェクトを取得
Graphics graphics = e.Graphics;
graphics.DrawEllipse(pen, x + start.X, x + start.Y, r, r);
}
}
動画を再生するにはvideoタグをサポートしたブラウザが必要です
ピクセルでは小さすぎて見にくかったので小さい円形の物体を動かすようにしました。Timerクラスを使ってフレーム(コマ送り)の速さを設定します。Intervalフィールドの値は次のフレームが開始されるまでのミリ秒です。多くのゲームやムービーなどで採用されている速さは60fps(1秒間に60コマ)なので、1000÷60=16.666
でだいたい16が近似値になるかと思います。Update()メソッドの中には、ループのインクリメント処理を切り出したものを書きます。
続いては円に沿って回転する物体を描画します。
public partial class Form1 : Form
{
Point start;
Pen pen;
float radius;
float r;
int x;
bool isCountUpX;
bool isPositiveNum;
public Form1()
{
InitializeComponent();
start = new Point(200, 200);
pen = new Pen(Color.Black, 1);
radius = 100; //物体が動く軌跡の半径
r = 8; //物体の半径
x = (int)-radius;
isCountUpX = true;
isPositiveNum = true;
//Timer
Timer timer = new Timer();
timer.Interval = 16;
timer.Tick += new EventHandler(Update);
timer.Start();
}
private void Update(object sender, EventArgs e)
{
Invalidate();
if (isCountUpX && (x <= radius))
{
//xが左から右
x++;
if(x == radius)
{
isCountUpX = false;
if (isPositiveNum)
{
isPositiveNum = false;
} else
{
isPositiveNum = true;
}
}
}
if(!isCountUpX && ((int)-radius <= x))
{
//xが右から左
x–;
if((int)-radius == x)
{
isCountUpX = true;
if (isPositiveNum)
{
isPositiveNum = false;
}
else
{
isPositiveNum = true;
}
}
}
}
protected override void OnPaint(PaintEventArgs e)
{
//Graphicsオブジェクトを取得
Graphics graphics = e.Graphics;
if (isPositiveNum)
{
//yが正の数
graphics.DrawEllipse(pen, x + start.X, (int)(Math.Sqrt(Math.Pow(radius,
2) – Math.Pow(x, 2))) + start.Y, r, r);
}
if (!isPositiveNum)
{
//yが負の数
graphics.DrawEllipse(pen, x + start.X, (int)-(Math.Sqrt(Math.Pow(radius,
2) – Math.Pow(x, 2))) + start.Y, r, r);
}
}
}
動画の再生にはvideoタグをサポートしたブラウザが必要です
xが -(半径) ≤ x ≤ 半径
の範囲を取りうることと、yが取りうる値に正負があることを考慮してこのようになりました。xがこの範囲を往復するように動き、右端と左端にくるとyの正負が逆転するようにしています。
円の軌跡のスピードが一定じゃないのはなぜ?
先ほどの回転する物体の動きをよく見ると、軌跡を辿るスピードが一定ではないように見えます。点が円の上部・下部付近を通過するときに比べ、左端・右端付近を通過するときの方がスピードが速くなっています。
これはグラフの軌跡を描くための変数として、円の関数のx座標だけを変化させているためです。x座標の値を一定の速さで変化させていますが、グラフが円形のため現在のフレームから次のフレームに移るときに点が移動する距離が、円周のどの位置にいるかによって変わるからです。
例えば傾きが異なる2本の直線グラフで、それぞれのx座標の値を同じ量加算してみます。
動画の再生にはvideoタグをサポートしたブラウザが必要です
傾きが大きい直線グラフの方が物体のスピードが速いですね。傾きが大きい直線グラフの方が、xの増加量に対するyの増加量が大きくなるためです。点の移動距離が大きくなるわけですね。
円周上のある点の付近を通過するときの点の動きは、円の接線となる直線グラフ上での移動に近い動きであると考えられます。円形グラフの上部に近いところの接線よりも左端・右端に近いところの接線の方が傾きが大きくなりますのでyの増加量が大きくなります。
円形グラフをただ描画するだけであれば問題ないのですが、敵キャラや弾の動きに利用するとなると、一定の速度で回転する円を描きたいですね。
次回は一定速度で円運動する弾を作ってみましょう。