グラフに合わせて自動的に移動する図形を作る
前回の記事で、ループを使ってグラフを描画しました。しかし円形グラフの円周上の点のx座標を加算したため、物体が移動するスピードが一定にならないという問題がありました。
これを一定のスピードにする場合、変化させる変数にxやyをそのまま使うのではなく、「媒介変数」を利用します。本記事では媒介変数を使って円運動する物体を描いていきます。
目次 Table of Contents
媒介変数を使って円の公式を分解する
前回は円の公式を使って円運動する物体を描画しましたが、物体のスピードが一定になりませんでした。Update()メソッドでxをインクリメントしていたのが原因です。こうしたグラフをいい感じに動かすには、x座標の変化とy座標の変化をそれぞれ別の関数を使って分解してやる必要があります。このときそれぞれの関数で共通で使われる変数のことを「媒介変数」といいます。では媒介変数を使ってx座標とy座標それぞれ分解して表してみましょう。
円の場合、円周上にある点の座標は((半径 * cosθ), (半径 * sinθ))になりますので、媒介変数として中心角θが使えます。
x = 半径 * cosθ
y = 半径 * sinθ
これで物体の位置が決まりますので、あとはUpdateメソッドで角度θを変化させてやればいいですね。一周(360°)したら再び0に戻してやればいいだけなので、場合分けも少なくて簡単です。
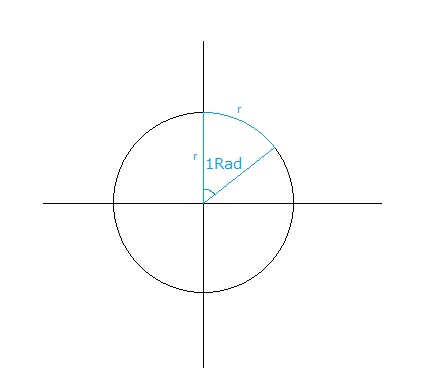
次の章のサンプルコードでは、角度θを「°」として扱っていますが、実際の計算時にはラジアンに変換して計算する必要があります。「1ラジアン」とは「円周の長さが円の半径と等しいときの、弧の中心角」です。半径をrとすると円周は2πrで、これを長さrで分割しますので円全体から扇形は2πr / r = 2π(個)取れることになります。
円の軌跡に沿って弾を一定速度で回転させる
それでは媒介変数を利用して、弾の回転運動を作ってみます。前章で使った、Updateメソッドを使用し角度の変数をインクリメントします。
public partial class Form1 : Form
{
Point start;
Pen pen;
float r; //物体の半径
double sin;
double cos;
float paramX;
float paramY;
float radius; //物体の軌跡の半径
int parameter; //媒介変数
public Form1()
{
InitializeComponent();
start = new Point(200, 200);
pen = new Pen(Color.Black, 1);
r = 8; //物体の半径
sin = Math.Sin(parameter * (Math.PI / 180));
cos = Math.Cos(parameter * (Math.PI / 180));
paramX = (float)(cos * radius) + start.X;
paramY = (float)(sin * radius) + start.Y;
radius = 100;
parameter = 0;
//Timer
Timer timer = new Timer();
timer.Interval = 16;
timer.Tick += new EventHandler(Update);
timer.Start();
}
private void Update(object sender, EventArgs e)
{
Invalidate();
parameter += 4;
if(parameter == 360)
{
parameter = 0;
}
sin = Math.Sin(parameter * (Math.PI / 180));
cos = Math.Cos(parameter * (Math.PI / 180));
paramX = (float)(cos * radius) + start.X;
paramY = (float)(sin * radius) + start.Y;
}
protected override void OnPaint(PaintEventArgs e)
{
//Graphicsオブジェクトを取得
Graphics graphics = e.Graphics;
graphics.DrawEllipse(pen, paramX, paramY, r, r);
}
}
動画を再生するにはvideoタグをサポートしたブラウザが必要です
x座標をインクリメントしたときと違い、一定の速度で物体が回転するようになりました。
媒介変数を使って色々なグラフを作ってみよう
媒介変数を使って色々なグラフを自由に作ることができます。あれこれ関数をいじって、いい感じの動きのグラフができたら採用、という感じで遊んでみるのもいいかもしれません。という前フリをしましたがいい感じのものが思いつきませんでしたので、ここではよく知られる数学のグラフから「インボリュート曲線」を紹介します。これは固定した糸巻きから糸をたるまないようにほどいていったときの糸の終端部分が描く軌跡、だということです。
public partial class Form1 : Form
{
Point start;
Pen pen;
float r; //物体の半径
double sin;
double cos;
float paramX;
float paramY;
int parameter; //媒介変数
float rad;
Bitmap p;
List<Point> listPoint;
public Form1()
{
InitializeComponent();
start = new Point(200, 200);
pen = new Pen(Color.Black, 1);
r = 8; //物体の半径
rad = (float)(parameter * (Math.PI / 180));
sin = Math.Sin(rad);
cos = Math.Cos(rad);
parameter = 0;
paramX = (float)(10 * (cos + rad * sin) + start.X) ;
paramY = (float)(10 * (sin – (rad * cos)) + start.Y);
p = new Bitmap(1, 1);
p.SetPixel(0, 0, Color.Black);
listPoint = new List<Point>();
listPoint.Add(new Point((int)paramX, (int)paramY));
//Timer
Timer timer = new Timer();
timer.Interval = 16;
timer.Tick += new EventHandler(Update);
timer.Start();
}
private void Update(object sender, EventArgs e)
{
Invalidate();
parameter += 4;
rad = (float)(parameter * (Math.PI / 180));
sin = Math.Sin(rad);
cos = Math.Cos(rad);
paramX = (float)(10 * (cos + rad * sin) + start.X);
paramY = (float)(10 * (sin – (rad * cos)) + start.Y);
listPoint.Add(new Point((int)paramX, (int)paramY));
}
protected override void OnPaint(PaintEventArgs e)
{
//Graphicsオブジェクトを取得
Graphics graphics = e.Graphics;
graphics.DrawEllipse(pen, paramX, paramY, r, r);
foreach(var value in listPoint)
{
graphics.DrawImage(p, value);
}
}
}
動画を再生するにはvideoタグをサポートしたブラウザが必要です
渦巻きグラフは色々使えそうですね。式もシンプルです。インボリュート曲線だと糸ほどきのグラフなのでやや物理的な感じになりますが、円運動する物体の回転半径をインクリメントしてやることでも渦巻き運動を作ることができます。この場合はもう少し機械的な渦巻き運動になるのかな~と思います。