微分をプログラミングで使う
微分・積分というとThe数学って感じがして嫌悪感を抱く人もいるかもしれません。僕もです。WebアプリやWebサイトなどの制作で微分・積分を使うことはあまりないかもしれませんが、ゲームプログラミングではかなり使用頻度が高い定理のようです。とはいえ、学生時代の数学のように難問をゴリゴリ解かされるようなものではなく、シンプルなコードで扱えるのでなかなか面白いです。本記事では簡単な微分のコーディングと、微分がどんなところで使われているのかについて調べたことを備忘録として残しておきます。サンプルコードはC#です。
目次 Table of Contents
微分って何?
微分とは「傾き」です。
y = a * x みたいな比例のグラフは直線グラフなので、グラフ上のどこをとっても傾きは一定です。では反比例や放物線のような曲線のグラフの傾きって何ってことになりますね。こうした曲線のグラフのある一点における傾きを求めることを微分するといい、求めた値をその点における微分係数といいます。
微分は次のように考えます。
・グラフ(f(x))上のある一点((x, f(x)))と、そこからX軸方向にhだけ進んだ点を結んだ直線の傾きを求める。
・hを限りなく0に近づけていった値は、まあほぼ点(x, f(x))における傾きと言ってもいいんじゃね?
こんな感じの考え方ですね。
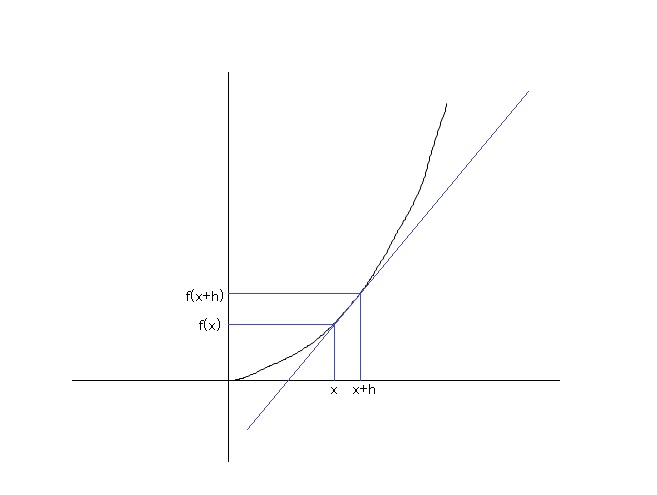
これを定義通りに実装して確認してみます。
Funcは元になる式 y = x2 、Derivativeはその微分係数を求める式です。 x2 を微分すると 2x ですので、x == 10のときの傾き(微分係数)は20になるはずです。距離hをだんだん小さくしていって、結果を比べてみます。
static float Func(float x)
{
return x * x;
}
//導関数(Derivative)
static float Derivative(float x, float h)
{
return (Func(x + h) – Func(x)) / h;
}
List<Label> listlabel = new List<Label>();
public Form1()
{
InitializeComponent();
for(int i = 0; i < 20; i++)
{
Label label = new Label();
label.Location = new Point(0, i * 20);
label.AutoSize = true;
label.Text = “label” + i + ” : “;
listlabel.Add(label);
this.Controls.Add(label);
}
listlabel[0].Text += Derivative(10, 0.1f);
listlabel[1].Text += Derivative(10, 0.01f);
listlabel[2].Text += Derivative(10, 0.001f);
}
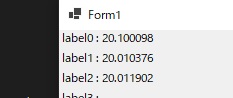
hを小さくしていくと、理論値に近づいていっているのがわかりますね。この微分を実装するコードは受け売りなんですが、簡単に書けて面白いな~と思います。
微分ってプログラミングではどんなところで使うの?
WebサイトやWebアプリのプログラミングでは微分を使うことはあまりないかもしれません。よく使いそうなジャンルだとゲームとかでしょうか。アクションゲームとかで、丸みのある坂道に立っているとだんだんずり落ちてくる処理、とか?傾きの大きさによって落ちる速度を変えてやることができそうですね。キャラクターの体の向きとか目線の方向とかも、微分で求めた傾きを元に処理できそうです。
その他に、ちょっと難しいですがシェーダーや画像のぼかし効果などのエフェクトを作るときにも、微分が使われるようです。以下の例では、緑色の線分は(0, 0)と(1, 1)で折れ曲がっています。
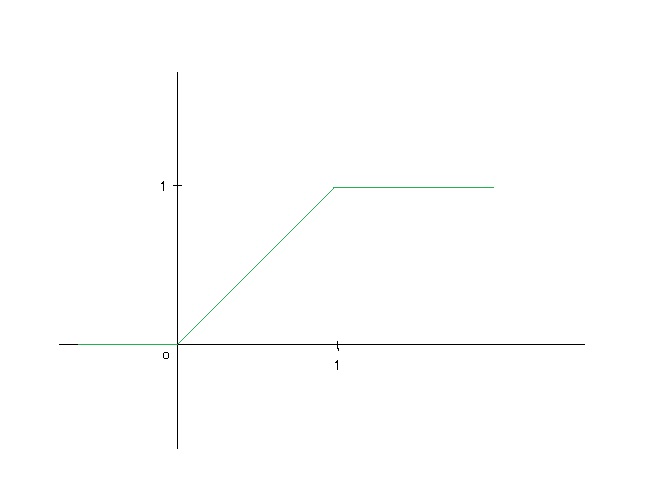
この折れ曲がって角ばっている部分をなめらかにつなげてやりたいな~っというようなときに微分の考え方が使われます。(0, 0)から(1, 1)までの直線を、以下のような曲線グラフに変換してやればなめらかに見えそうです。
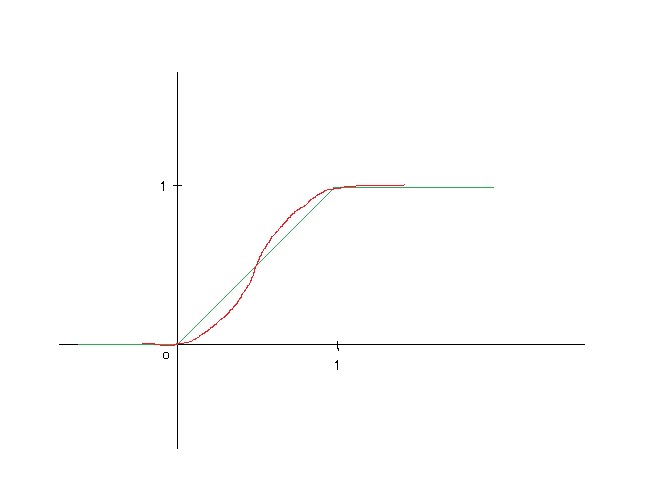
この曲線グラフをg(x)とし、図からわかるいくつかの条件をあげてみます。
・(0, 0)をとおる
・(1, 1)をとおる
・(½, ½)をとおる
・(0, 0)での傾きが0、つまりg’(0) = 0
・(1, 1)での傾きが0、つまりg’(1) = 0
判明している条件が5つありますので、不明な変数は5つまで用意できます。仮に
g(x) = a * x4 + b * x3 + c * x2 + d * x + e
と定義して、条件をもとにa~eを求めてg(x)を求めます。実際にコーディングした結果、以下のようになりました。角ばった線の輪郭がなめらかになった気がしますねw実際にはもっと複雑なアルゴリズムを組み合わせていると思いますが、考え方はこんな感じみたいです。面白いですね、微分(^^)
Windows Formsのコードを載せておきます。サンプルコードでは、Y軸が下向きだったり原点が描画画面の左上点だったりして見づらいので、少し手を加えています。また(0, 0)と(1, 1)では小さくて見えないので、(0, 0)と(200, 200)からg(x)を求めています。(1ピクセルの範囲では視認できないので。)
public partial class Form1 : Form
{
Bitmap p;
Bitmap p1;
Bitmap p2;
static Point origin = new Point(300, 300);
static float FuncF(float x)
{
//return -x;
return -x + origin.X + origin.Y;
}
static float FuncG(float x)
{
//return -(x * x * (3f – 2f * x));
return -((-1f * x * x * x / (2f * 100f * 100f)) + 3f * x * x / 200f);
}
public Form1()
{
InitializeComponent();
p = new Bitmap(1, 1);
p1 = new Bitmap(1, 1);
p2 = new Bitmap(1, 1);
}
protected override void OnPaint(PaintEventArgs e)
{
Graphics graphics = e.Graphics;
p.SetPixel(0, 0, Color.Black);
p1.SetPixel(0, 0, Color.Green);
p2.SetPixel(0, 0, Color.Red);
for(int i = 0; i < 600; i++)
{
//X, Y軸
graphics.DrawImage(p, i, 300);
graphics.DrawImage(p, 300, i);
}
for (int i = origin.X; i < 200 + origin.X; i++)
{
//FuncF
graphics.DrawImage(p1, i, FuncF(i));
}
for (int i = -200 + origin.X; i < origin.X; i++)
{
//折れた左の線分
graphics.DrawImage(p1, i, FuncF(origin.X));
}
for(int i = 200 + origin.X; i < (400 + origin.X); i++)
{
//折れた右の線分
graphics.DrawImage(p1, i, FuncF(200 + origin.X));
}
for(int i = 0; i < 200; i++)
{
//FuncG
graphics.DrawImage(p2, i + origin.X, FuncG(i) + origin.Y);
}
}
}
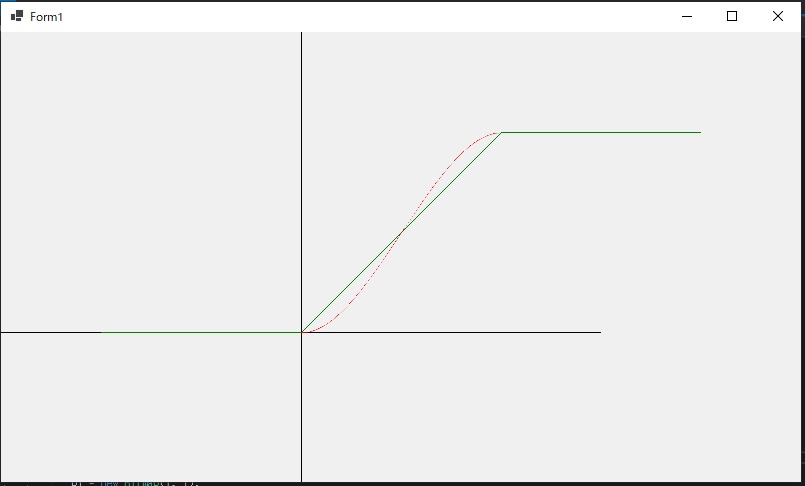
FuncGの計算時、originの座標を計算に入れていなかったので、ちょっと変になったけど。。。